Write a c++ program to find the first n prime numbers.
In this blog, we are going to create a program to find the first n prime numbers.
What are Prime numbers?
Numbers having only two factors, i.e. 1 and the numbers themselves, are known as Prime numbers.
Example: 2,3,5,7,11,13..etc.
Find 1-N prime number in C++
Approach 1: By formal definition, a number ‘n’ is prime if it is not divisible by any number other than 1 and n. In other words, a number is prime if it is not divisible by any number from 2 to n-1.
Approach 2: To check if a number is prime or not, do we really need to iterate over the entire number form from 2 to n-1? We already know that the number ‘n’ is not divisible by any number greater than ‘n/2’. So by this logic, we only need to iterate over 2 to n/2 because a number greater than n/2 cannot divide n. Time complexity: O(N^2), Space complexity: O(1)
Approach 3: If the number ‘n’ is not divisible by any number less than or equal to the square root of n, it will not be divisible by any other number greater than the square root of n. So we only need to check the square root of n.
Algorithm to find n prime numbers
- First, take the number N as input.
- Then use a loop to iterate numbers from 1 to N.
- then check every number whether it is prime or not, if it is prime print it.
C++ program to find n prime numbers
// C++ program to display
// Prime numbers till N
#include <bits/stdc++.h>
using namespace std;
// Function to check if a
// given number is prime
bool isPrime(int n)
{
// Since 0 and 1 is not
// prime return false.
if(n == 1 || n == 0) return false;
// Run a loop from 2 to n-1
for(int i = 2; i < n; i++)
{
// if the number is divisible by i,
// then n is not a prime number.
if(n % i == 0) return false;
}
// Otherwise n is a prime number.
return true;
}
// Driver code
int main()
{
int N = 100;
// Check for every number from 1 to N
for(int i = 1; i <= N; i++)
{
// Check if current number is prime
if(isPrime(i))
{
cout << i << " ";
}
}
return 0;
}
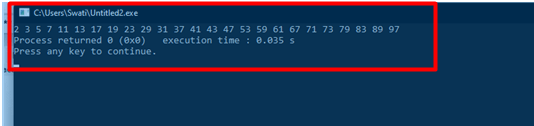
Output: