In this section of the tutorial, we will discuss the 2D Array in Data Structure and we will learn the properties of 2D Array, important operations on Array such as mapping a 2D Array into a 1D Array and finding the address of a random 2D Array element which will be used thoroughly later in this Data Structure tutorial.
Now let’s move further to the introduction of the collection of similar data items in two dimensions in a Data Structure, i.e. 2D Array.
What are 2D Arrays in Data Structure?
Arrays can be created of more than one dimension for storing a list of values in a tabular form in terms of rows and columns. The exact limit of the number of dimensions is determined by the compiler.
Here, we will mainly focus on Two Dimensional Array or 2D Array in Data Structure.
The general form of a 2D Array: datatype array_name[s1][s2];
- Here, datatype indicates the type of data that is to be stored in a 2D Array.
- array_name indicates the name of the 2D Array.
- s1 and s2 indicate the respective sizes of each dimension in the 2D Array.
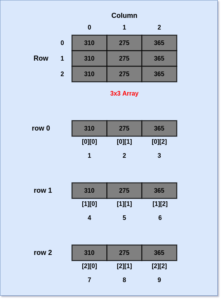
In the above diagram, we can see the representation of a 2D Array in memory.
Example:
int Table[3][4];
We will understand how we can use a 2D Array with the help of an example given below.
Example: Program to read a matrix and print its transpose using Arrays.
Sample code:
#include<stdio.h>
int main()
{
int i,j,a[3][3],b[3][3];
printf("Enter the values below: \n");
for ( i = 0; i < 3; i++)
{
for ( j = 0; j < 3; j++)
{
printf("a[%d][%d]: ",i,j);
scanf("%d",&a[i][j]);
}
}
printf("\nEntered matrix is: \n");
for ( i = 0; i < 3; i++)
{
printf("\n");
for ( j = 0; j < 3; j++)
{
printf("%d\t",a[i][j]);
}
}
for ( i = 0; i < 3; i++)
{
for ( j = 0; j < 3; j++)
{
b[i][j]=a[j][i];
}
}
printf("\nTranspose of the matrix is: \n");
for ( i = 0; i < 3; i++)
{
printf("\n");
for ( j = 0; j < 3; j++)
{
printf("%d\t",b[i][j]);
}
}
return 0;
}
Output:
Entered matrix is: 1 2 3 4 5 6 7 8 9 Transpose of the matrix is: 1 4 7 2 5 8 3 6 9
Now, we have come across the declaration, initialization, and accessing of 2D Array in the above example. It is similar to the declaration, initialization, and accessing of the 1D Array that we have seen in the previous tutorial.
Declaring a 2D Array
In a 2D Array, we can define a table or matrix having ith row and jth column before we use it to store data items into it. We will look into an example to understand this.
Example: arr[4][3]
- We can consider the table as a matrix having four rows and three columns.
- Each row and column representing a distinct set of data values.
The general form of declaring a 2D Array in C language:
type array_name [row_size][column_size];
Important note: There are different declaration styles of the sizes of row and column in languages other than C.
Initializing a 2D Array
Similar to the initialization of 1D Array, we can declare and initialize a 2D Array with a list of initial values enclosed in braces. We will look into an example to understand this.
Example: int arr[2][3] = {0,0,0,1,1,1};
- Here, the above statement initializes the elements of the first row to zero and the second row to one.
- The initialization is done row by row.
The above example statement can also be written as:
int arr[2][3] = {{0,0,0},{1,1,1}};
In the above example statements, the syntax has commas after each set of braces that closes off a row, except for the last row.
Accessing 2D Array elements
We can access elements of a 2D Array in a similar way we access a 1D Array element. As each cell inside a 2D Array has a unique index number in terms of row and columns assigned to it. We can use it to access the element and hence the data value present inside it.
We will see an example to understand how we can access a 2D Array in a program.
Example: Program to add two matrices and print their sum in the third matrix using Arrays.
Sample code:
#include<stdio.h>
int main()
{
int i, j,r=2,c=2,A[r][c],B[r][c],C[r][c];
printf("Enter elements of first Matrix A: \n");
for(i = 0; i < r; i++)
{
for(j = 0; j < c; j++)
{
scanf("%d", &A[i][j]);
}
}
printf("\nEnter elements of Matrix B: \n");
for(i = 0; i < r; i++)
{
for(j = 0; j < c; j++)
{
scanf("%d", &B[i][j]);
}
}
printf("\nMatrix C:\n");
for(i = 0; i < r; i++)
{
for(j = 0; j < c; j++)
{
C[i][j]=A[i][j]+B[i][j];
printf("%5d ",C[i][j]);
}
printf("\n");
}
return 0;
}
Output:
Enter elements of first Matrix A:
1
2
3
4
Enter elements of Matrix B:
1
2
3
4
Matrix C:
2 4
6 8
In the above program, we have accessed each element for storing the data values input by the user using the format &A[i][j] and &B[i][j], where i and j represent the rows and columns of the 2D Arrays A and B.
Memory allocation of a 2D Array
The memory allocation of the stored data valued in a 2D Array works in the way that the subscripts that represent the rows and columns of the 2D Array are used to map the way the data values are laid out in the memory.
- The elements of the 2D Array are stored contiguously in increasing memory locations.
- In an Array, if we consider the memory as a row of bytes, then the first element will be stored at the left end and the last element is stored at the right end of the allotted memory.
- Similarly, in a 2D Array, the data values are stored in the memory in a row-wise manner, starting from the first row and ending at the last row, considering each row a single array.
In the diagram above, we can see the memory allocation of a 2D Array in laying out and storing data values in the memory.
Mapping a 2D Array into a 1D Array
A 2D Array can be mapped into a 1D Array as the representation of 2D Array in memory space is from the user’s point of view. So 2D Arrays are implemented in a relational database table such as in Data Structure, in the computer’s memory.
- The storage distribution of the 2D Array is similar to the 1D Array.
- The multiplication of the number of rows and the number of columns is equal to the size of the 2D Array.
- It is represented in the memory space in the same individual manner.
- This is required to store a 2D Array into a 1D Array.
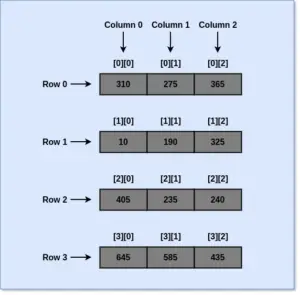
Example: A 2D Array of 4×4 size is illustrated in the diagram given below. We will map the given 2D Array into a 1D Array to understand its distribution in the memory space.
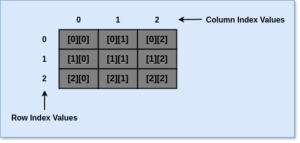
Row Major Order
As we know that the data values are stored in the memory space contiguously. We can follow the Row Major Order to map the 2D Array into a 1D Array.
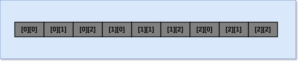
- Here, the 1st row of the 2D Array is stored in the memory space.
- Then, the 2nd row of the 2D Array is stored in the memory space.
- Then, this process repeats until the last row of the 2D Array is stored in the memory space.
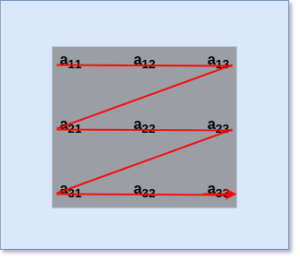
The flow of Row Major Order is depicted above.
Column Major Order
Similarly, in the Column Major Order, the columns of the 2D Array is stored in the memory space contiguously. We can follow the Column Major Order to store a 2D Array in the memory space in a similar way as we did in Row Major Order.

- Here, the 1st column of the 2D Array is stored in memory space.
- Then, the 2nd column of the 2D Arrau is stored in the memory space.
- Then, this process repeats until the last column of the 2D Array is stored in the memory space.
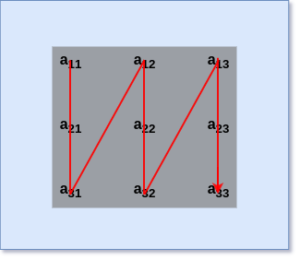
The flow of Column Major Order is depicted above.
Address of a random 2D Array element
As we know, there exist two ways of storing a 2D Array in the memory space, i.e. Row Major Order and Column Major Order. So, there are also two similar ways to find the address of any random 2D Array element.
By Row Major Order
For a 2D Array arr[m][n], where m and n represent the number of rows and the number of columns respectively. Then, the address of any element arr[i][j] present in the 2D Array that is stored in row major order can be calculated as follows:
Address(arr[i][j]) = B. A. + (i * m + j) * size
- Here, B.A. specifies the address of the first element arr[0][0] or the base address of the 2D Array.
By Column Major Order
For a 2D Array arr[m][n], where m and n represent the number of rows and the number of columns respectively. Then, the address of any element arr[i][j] present in the 2D Array that is stored in column major order can be calculated as follows:
Address(arr[i][j]) = ((j*n)+i)*Size + B.A.
Here, B.A. specifies the address of the first element arr[0][0] or the base address of the 2D Array.
In the next section of the tutorial, we will discuss the Searching in Data Structure, which includes two main techniques of searching, i.e. Linear Search and Binary Search. These Searching Techniques are important in solving Data Structure problems.
