In this section of the tutorial, we will discuss the Binary Search in Data Structure which is used to locate an item in an ordered collection of data items or array. We will discuss the Algorithm of Binary Search and its implementation using examples and illustrated diagrams for better understanding.

Now, let’s move further to the introduction of Binary Search in Data Structure.

What is Binary Search in Data Structure?

In the Binary Search, we compare the key with the item in the middle position of the array of items. Generally, Binary Search is used to handle a large volume of data items contrary to the Linear Search. But the Binary Search is used only if the array is sorted, otherwise, we use Linear Search to sort the array.

• Binary Search is usually used whenever we have more than 16 items in an array.
• Binary Search is used when we have a sorted array.
• In Binary Search, we eliminate half the list if the target is not present in there by comparing the data items by the middle item in the list.
• This process of comparison is repeated until half of the remaining list is eliminated with each test.
• And this process continues and eventually, we either find the target or determine that it is not present in the list.

Binary Search is comparatively faster than Linear Search as it only searches the part of the list where the chances of finding the target are high, unlike Linear Search. And hence, Binary Search is much faster than Linear Search. Binary Search can be used to search a target in a large number of data items, unlike Linear Search which is used to search only a few data items.

Binary Search

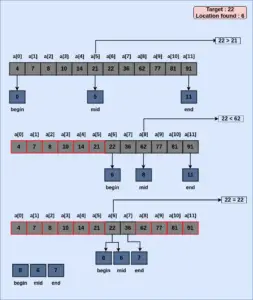
The above-illustrated diagram shows an ordered list where Binary Search is implemented.

Further, we will learn about the concept used in Binary Search in searching for a target.

Concept used in Binary Search

As we know that Binary Search is used to find the position of a data value (target) in an ordered list and it is more efficient than Linear Search. Now we will understand the logic used in implementing the Binary Search to search a list of data items.

• Binary Search tests the data in the element at the middle of the array to find whether the target is in the first or the second half of the list.
• If the target is present in the first half, we need not check the second half.
• If the target is present in the second half, we need not check the first half.
• For each time we compare the middle item of the list with the first and last element in the list.
• We take half the list into consideration and eliminate the other half of the list.
• This process continues until we find the target value or we are sure that the target is not present in the list.

Now to implement Binary Search, we need different variables to perform different tasks in the operation.

• Three variables are assigned to find the middle of the list.
• One variable to identify the beginning of the list.
• One variable to identify the middle of the list.
• One variable to identify the end of the list.
• After that, we analyze two cases using this concept, i.e. target is present in the list and target is not present in the list.

Algorithm of Binary Search

Now we will discuss the algorithm of Binary Search which is important to understand and implement the Binary Search for solving problems.

Similar to the algorithm of Linear Search, Binary Search is also designed to find the location of the desired data item but in a more efficient way.

The algorithm of Binary Search is as follows:

Algorithm BinarySearch (list, last, target, addr)
set begin to 0
set end to last
loop (begin <= end)
   set mid to (begin + end) / 2
   if (target > list[mid])
      set begin to (mid + 1)
   else if (target < list[mid])
      set end to mid - 1
   else
      set begin to (end + 1)
   end if
end loop
set addr to mid
if (target equal list [mid])
   set found to true
else
   set found to false
end if
return found
end BinarySearch

• Here, list is in ordered form and it must have at least one value last is index to the largest data item in the list.
• last is index to largest data item in the list.
• target is the value of the element to be searched in the list.
• addr is the address of index in calling algorithm.

Working of Binary Search Algorithm

The first three parameters define the list and the target we are aiming for and the last parameter holds the address inside which we will store the index value of the target if found. If the target is not found in the list, the loop is terminated and any random index is returned.

The working of the algorithm of Binary Search given above is as follows:

• list should be ordered.
• list must have at least one element.
• last is the index value of the largest element of the list.
• target is the value of the element to be searched.
• addr specifies the address of the index in calling algorithm.
• If the target is found in the list, addr is assigned to index to target element and found is set true.
• If the target is not found in the list, addr is assigned to element below or above of the target and found is set false.
• Now, found is returned true or false.

Time and Space Complexity of Algorithm

Binary Search Implementation

Now that we understand the concept of Binary Search and also we have written the algorithm of Binary Search, now we can implement Binary Search in a programming language to perform the operation. Here, we will implement Linear Search in C and C++

Implementation in C

Code:

#include<stdio.h>
int main()
{
    int arr[12]={10,20,30,40,50,60,70,80,90,100,110,120};
    int i=0,j,k=11;
    int value,check=0;
    printf("Enter a data to search:  ");
    scanf("%d",&value);
    while(i<=k)
    {
        j=(i+k)/2;
        if(arr[j]==value)
        {
            check=1;
            break;
        }
        else
        {
            if(arr[j]<value)
                {
                    i=j+1;                    
                }
            else
                k=j-1;  
        }
    }

    if(check==1)
        printf("Data found\n");
    else
        printf("Data not found\n");
    return 0;
}

Output:

Enter a data to search:  110
Data found

Implementation in C++

Code:

#include<iostream>
using namespace std;
int main()
{
    int arr[12]={10,20,30,40,50,60,70,80,90,100,110,120};
    int i=0,j,k=11;
    int value,check=0;
    cout<<"Enter a data to search: ";
    cin>>value;
    while(i<=k)
    {
        j=(i+k)/2;
        if(arr[j]==value)
        {
            check=1;
            break;
        }
        else
        {
            if(arr[j]<value)
                {
                    i=j+1;                    
                }
            else
                k=j-1;  
        }
    }

    if(check==1)
        cout<<"Data found at location arr["<<j<<"]\n";
    else
        cout<<"Data not found\n";
    return 0;
}

Output:

Enter a data to search: 70
Data found at location arr[6]

In the next section of the tutorial, we will discuss Sorting in Data Structures and the different sorting techniques used in performing operations in detail.