In this blog, we will create a program to count all the composite numbers in an array using C++.

What are Composite numbers?

Composite numbers are numbers with more than two factors. Numbers can be classified based on the number of factors they have. If a number has only two factors – 1 and the number itself, then it is a prime number. However, most numbers have more than two factors and are called composite numbers.

Algorithm to count Composite numbers in C++

• Declare one array and three variables.
• First, take two inputs for the size of the array and another to take the elements in the array.
• Take two for loops, one is for input and another for loop is to give logic and condition.
• Take if, else if, and if statements.
• Print the appropriate message.

C++ program to count composite numbers in an array in C++

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
// Function to find and return the
// the count of the composite numbers
int compcount(int ar[], int num, int* sum)
{
   // storing the largest element of the array
   int max_val = *max_element(ar, ar + num);
   // Using sieve to find all prime numbers
   // less than or equal to max_val
   // Create a boolean array "prime[0..n]". A
   // value in prime[i] will finally be false
   vector<bool> pr(max_val + 1, true);
   // setting the values of 0 and 1 as
   // true for prime.
   pr[0] = true;
   pr[1] = true;
   for (int p = 2; p * p <= max_val; p++){
      // If prime[p] is not changed, then
      // it is a prime
      if (pr[p] == true){
         // Update all multiples of p
         for (int i = p * 2; i <= max_val; i += p){
            pr[i] = false;
         }
      }
   }
   // Count all composite
   // numbers in the arr[]
   int ans = 0;
   for (int i = 0; i < num; i++){
      if (!pr[ar[i]]){
         ans++;
         *sum = *sum + ar[i];
      }
   }
   return ans;
}
// Driver code
int main(){
   int ar[] = { 1, 2, 3, 4, 5 };
   int num = sizeof(ar) / sizeof(ar[0]);
   int sum = 0;
   cout << "Count of Composite Numbers = "<< compcount(ar, num, &sum);
   cout << "\nSum of Composite Numbers = " << sum;
   return 0;
}

Explanation of the code

• Enter an array of positive integers
• Calculate its size
• Initialize the sum variable to store the sum of the composite numbers.
• Store the maximum value present in the field in a variable
• Calculate the prime numbers to the maximum value.
• Iterate through the entire array and check if the number is prime or not. If the number is not prime, it will be a composite number, and if so, increment the composite number by 1 and add its value to the sum.

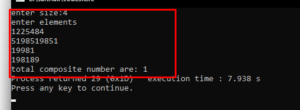
Output of the code