In this section of the tutorial, we will discuss the use of Graph in Data Structure which will include the types of graph, graph representation, DFS Algorithm, BFS Algorithm, Prim’s Algorithm, Kruskal’s Algorithm and its implementation in programs.
Now let’s move on further to the introduction of Graphs in Data Structure.
What are Graphs in Data Structure?
Graphs are very useful data structures and they are often used to solve complex routing problems like designing and routing airlines among the airports they operate into.
Similarly, they are used in routing messages over a computer network from one to another node.
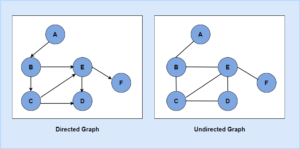
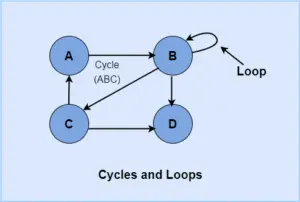
Below are some important terminologies used in graph:
Graph: It is a collection of nodes.
Vertices: It is the fundamental unit of building a graph.
Lines: It is a collection of segments.
Adjacent vertices: They are two connected vertices in a graph joined by a path of length 1.
Degree of a vertex: It is the number of lines incident on the vertex.
Directed graph or digraph: A graph in which each line has a direction (arrow head) to its successor.
Undirected graph: A graph in which there is no direction of any of the lines are present.
Path: It is a sequence of vertices where each vertex is adjacent to the next vertex.
Cycle: It is a path having at least three vertices that starts and ends with the same vertex.
Loop: It is a special case of a cycle where a single arc begins and ends with the same vertex.
Graph Operations
These are some basic operations to perform the Graph Operations in Data Structure. Although, any other operation can also be carried out and added to the data structure.
Insert vertex
This operation adds a new vertex in a graph.
- When we insert a vertex in a graph, it is disjoint, it is not connected to any other vertex in the list.
- However, adding a vertex in the first step of the operation followed by connecting the vertex to other vertices.
Delete vertex
This operation deletes or removes a vertex from the graph.
- When a vertex is removed, all the connecting edges are also removed with it.
Insert edge
This operation connects a vertex to a destination vertex.
- If we come across a situation where a vertex needs multiple edges, add an edge must be called once for each adjacent vertex.
- For adding an edge, two vertices must be specified.
- As for a digraph, one of the vertices must be specified as the source and the other as the destination.
Delete edge
- This operation deletes or removes one edge from a graph.
Graph Traversal Methods
There could be a situation where we need to visit all the vertices in a graph. Here, we use the graph traversal methods to visit the vertices in a graph.
Here, we will discuss two standard graph traversal methods, i.e. depth-first traversal and breadth-first traversal.
Depth-First Traversal
In depth-first traversal, before we move to an adjacent vertex we process all of a vertex’s descendants.
This kind of traversal is mostly used in graphs when the graph is in the form of a tree.
In the diagram below we can see the depth-first traversal of a graph.
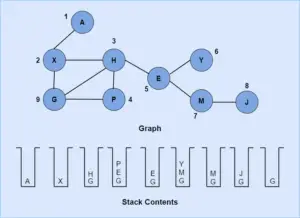
- We start by pushing the first vertex, A, into the stack.
- Then we loop and pop the stack.
- After the vertex is processed, we push all the adjacent vertices into the stack.
- Once the stack is empty, it means the traversal is completed.
Breadth-First Traversal
In breadth-first traversal, before we go the next level we process all the adjacent vertices of a vertex.
In the diagram below we can see the breadth-first traversal of a graph.
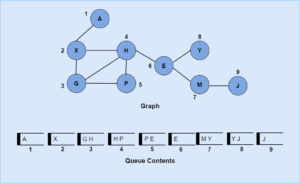
- We start by enqueuing vertex A in the queue.
- Then we loop and dequeue the queue.
- Then we process the vertex from the front of the queue.
- After the processing is done, we place all of its adjacent vertices into the queue.
- Once the queue is empty, it means the traversal is completed.
Graph Algorithms
The nature of the program states what type of graph applications it needs. So, it sometimes becomes necessary to write a clean algorithm that returns the vertex count or vertex’s indegree or outdegree or any other purpose.
Here, we will discuss two such algorithms, i.e. Prim’s Algorithm and Kruskal’s Algorithm.
Prim’s Algorithm
Prim’s Algorithm is used to find the minimum spanning tree (MST) of a graph. This algorithm begins with a vertex and keeps on adding edges as we progress into the graph.
Prim’s Algorithm Pseudocode
Algorithm Prim(empty graph)
1 while empty graph is not a MST of graph loop
1 find an edge in graph that is in some MST of the graph, but not in empty graph
2 add edge to graph (unless edge makes a cycle)
2 end loop
3 return empty graph
End Algorithm
- We select a random vertex as the starting point.
- Then we initialize a minimum spanning tree.
- We find the edges that connect the other vertices.
- We find the minimum weight and add it to the spanning tree.
- We keep on adding edges until all the vertices are covered.
Kruskal’s Algorithm
Kruskal’s Algorithm is used to find the MST in a connected graph. The algorithm finds a subset of a graph and forms a tree with every vertex in it. The sum of the weight is minimum among all the spanning trees that can be possibly formed from this graph.
Kruskal’s Algorithm Pseudocode
Algorithm Kruskal(Graph)
1 int edgesAccepted = 0;
2 DisjSet s(NUM_VERTICES);
3 while (edgesAccepted < NUM_VERTICES – 1)
1 edge e = (u, v)
4 uset = s.find(u);
5 vset = s.find(v);
6 if (uset != vset)
1 edgesAccepted++;
2 s.unionSets(uset, vset);
End Algorithm
- Here, the algorithm first sorts all the edges from the lowest weight to the highest.
- Then the lowest weight of the edge is selected and it is added to the spanning tree.
- If the cycle is created, the edge is discarded.
- Then the edges are kept added until all the vertices are covered.
Program example to demonstrate the implementation of Graph Operations
Code:
#include <iostream>
#include <list>
#include <stack>
using namespace std;
class Graph
{
int V;
list<int> *adj;
void Fill_Order(int s, bool visitedV[], stack<int> &Stack);
void DFS(int s, bool visitedV[]);
public:
Graph(int V);
void Add_Edge(int s, int d);
void display();
Graph transpose();
};
Graph::Graph(int V)
{
this->V = V;
adj = new list<int>[V];
}
void Graph::DFS(int s, bool visitedV[])
{
visitedV[s] = true;
cout << s << " ";
list<int>::iterator i;
for (i = adj[s].begin(); i != adj[s].end(); ++i)
if (!visitedV[*i])
DFS(*i, visitedV);
}
Graph Graph::transpose()
{
Graph g(V);
for (int s = 0; s < V; s++)
{
list<int>::iterator i;
for (i = adj[s].begin(); i != adj[s].end(); ++i)
{
g.adj[*i].push_back(s);
}
}
return g;
}
void Graph::Add_Edge(int s, int d)
{
adj[s].push_back(d);
}
void Graph::Fill_Order(int s, bool visitedV[], stack<int> &Stack)
{
visitedV[s] = true;
list<int>::iterator i;
for (i = adj[s].begin(); i != adj[s].end(); ++i)
if (!visitedV[*i])
Fill_Order(*i, visitedV, Stack);
Stack.push(s);
}
void Graph::display()
{
stack<int> Stack;
bool *visitedV = new bool[V];
for (int i = 0; i < V; i++)
visitedV[i] = false;
for (int i = 0; i < V; i++)
if (visitedV[i] == false)
Fill_Order(i, visitedV, Stack);
Graph gr = transpose();
for (int i = 0; i < V; i++)
visitedV[i] = false;
while (Stack.empty() == false)
{
int s = Stack.top();
Stack.pop();
if (visitedV[s] == false)
{
gr.DFS(s, visitedV);
cout << endl;
}
}
}
int main()
{
Graph g(8);
g.Add_Edge(0, 1);
g.Add_Edge(1, 2);
g.Add_Edge(2, 3);
g.Add_Edge(2, 4);
g.Add_Edge(3, 0);
g.Add_Edge(4, 5);
g.Add_Edge(5, 6);
g.Add_Edge(6, 4);
g.Add_Edge(6, 7);
cout << "Connected Vertices:\n";
g.display();
}
Output:
Connected Vertices: 0 3 2 1 4 6 5 7
In the upcoming sections of the tutorial, we will practice programs on Data Structure which will cover topics like Searching, Sorting, Linked List, and Tree.
