In this section of the tutorial, we will learn the Merge Sort and its concept in Data Structure and the algorithm of Merge Sort in detail. We will understand the algorithm and the working principle using a few program examples

Now let’s move further to the detailed introduction of Merge Sort in Data Structure.

What is Merge Sort in Data Structure?

In Merge Sort, a sequence of elements are divided into two smaller parts and are individually sorted and then merged eventually into one sorted list. We will look into the points below to understand the merge sort in detail.

• In Merge Sort, a list of elements are sorted by first splitting into two halves.
• Then the independent sublists formed are sorted individually.
• Eventually, both the sublists are merged into a single list of sorted elements.
• The working of Merge Sort is completely based on Divide and Conquer Strategy that we have learnt earlier in this tutorial.
• In Divide and Conquer Strategy, a pool of data S is divided into two disjoint subsets S1 and S2. This is the step where we divide the list into two parts.
• Then these subsets S1 and S2 are sorted and the subsolutions are obtained. This is the step where we solve the two sublists individually.
• Eventually, we combine both the subsolutions obtained from the sublists or subsets, i.e. S1 and S2. This is the step where we combine both the solution to form one sorted list for the original problem S.

Now that we are familiar with the Merge Sort and it’s principle. Let’s dig deeper into the core concept involved in Merge Sort.

Concept used in Merge Sort

The concept involved in Merge Sort is quite simple as we have learnt the divide and conquer strategy in the previous section. It follows the technique of dividing, then solving, and then merging the solution to obtain a sorted list of elements.

We will look into the illustrated diagram and example to understand the concept behind Merge Sort in details.

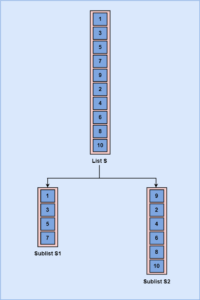
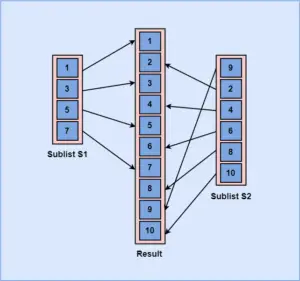
• Here, a list S is divided into two sublists, i.e S1 and S2.
• Now, we have to sort both the sublists.
• So, we compare the first element of S1 with the first element of S2 and write the smaller one to an independent list, i.e. Result.
• We then compare the second element of S1 with the first element of S2, and write down the smaller one in the list, i.e. Result.
• This process of comparing and merging elements into the list continues till the entire list of elements is sorted.
• By now, we have understood the concept involved in Merge Sort. Let’s write the Algorithm for Merge Sort.

Merge Sort Algorithm

Now that we are familiar with the concept of Merge Sort, we can now develop an algorithm of Merge Sort before we put it into implementation.

Algorithm MergeSort
1 read list S and divide list S
2 read (sublist1 into S1)
3 read (sublist2 into S2)
4 loop (not end sublist1 OR not end sublist2)
    1 if (S1 key <= S2 key)
        1 write (S1 to Result)
        2 read (sublist1 into S1)
        3 if (end of sublist1)
            1 set S1 key to infinity
        4 end if
    2 else
        1 write (S2 to Result)
        2 read (sublist2 into S2)
        3 if (end of sublist2)
            1 set S2 key to infinity
        4 end if
    3 end if
5 end loop
6 close files
end MergeSort

Working of Merge Sort

The working of the Merge Sort in accordance to the above Algortihm is as follows:

• The list S is read and divided into two parts, i.e. sublist1 and sublist2.
• Initially, input files are sorted. And sublist1 and sublist2 are read in S1 and S2 respectively.
• Now, loop is iterated till the end of each sublist S1 and S2.
• The key or current element from S1 and S2 is compared with conditions are if found to be true, then it is moved to list Result.
• The loop iterates till the end of both S1 and S2, and by now all the elements of S1 is compared with S2.
• Eventually, the input elements of S1 and S2 are merged and sequentially arranged in the list Result.

We will look into an illustrated diagram example to understand the working of Merge Sort step by step.

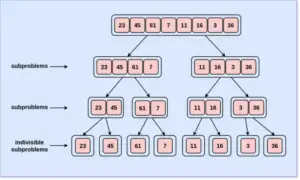
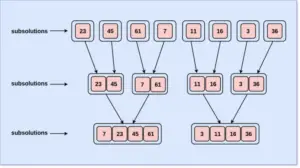
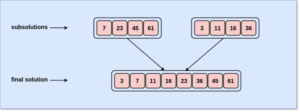
Time and Space Complexity of Algorithm

Merge Sort Implementation

Now that we understand the concept of Merge Sort and also we have written the algorithm of Merge Sort, now we can implement Merge Sort in a programming language to perform the operation. Here, we will implement the Merge Sort in C and C++

Implementation in C

Code:

#include <stdio.h>
void merge_sort(int *, int , int );
void merge(int *,int, int , int );
int main()
{
    int myarray[30], num;
    printf("Enter number of elements to be sorted: ");
    scanf("%d",&num);
    printf("Enter %d elements to be sorted: ",num);
    for (int i = 0; i < num; i++)
    {
        scanf("%d",&myarray[i]);
    }
    merge_sort(myarray, 0, num-1);
    printf("Sorted array\n");
    for (int i = 0; i < num; i++)
    {
        printf("%d ",myarray[i]);
    }
}
void merge_sort(int *arr, int begin, int end)
{
    int middle;
    if (begin < end)
    {
        middle=(begin+end)/2;
        merge_sort(arr,begin,middle);
        merge_sort(arr,middle+1,end);
        merge(arr,begin,end,middle);
    }
}
void merge(int *arr, int begin, int end, int middle)
{
    int i, j, k, c[50];
    i = begin;
    k = begin;
    j = middle + 1;
    while (i <= middle && j <= end)
    {
        if (arr[i] < arr[j])
        {
            c[k] = arr[i];
            k++;
            i++;
        }
        else
        {
            c[k] = arr[j];
            k++;
            j++;
        }
    }
    while (i <= middle)
    {
        c[k] = arr[i];
        k++;
        i++;
    }
    while (j <= end)
    {
        c[k] = arr[j];
        k++;
        j++;
    }
    for (i = begin; i < k; i++)
    {
        arr[i] = c[i];
    }
}

Output:

Enter number of elements to be sorted: 5
Enter 5 elements to be sorted: 54
97
51
26
-45
Sorted array        
-45 26 51 54 97

Implementation in C++

Code:

#include <iostream>
using namespace std;
void merge_sort(int *, int , int );
void merge(int *,int, int , int );
int main()
{
    int myarray[30], num;
    cout<<"Enter number of elements to be sorted:";
    cin>>num;
    cout<<"Enter "<<num<<" elements to be sorted:";
    for (int i = 0; i < num; i++)
    {
        cin>>myarray[i];
    }
    merge_sort(myarray, 0, num-1);
    cout<<"Sorted array\n";
    for (int i = 0; i < num; i++)
    {
        cout<<myarray[i]<<"\t";
    }
}
void merge_sort(int *arr, int begin, int end)
{
    int middle;
    if (begin < end)
    {
        middle=(begin+end)/2;
        merge_sort(arr,begin,middle);
        merge_sort(arr,middle+1,end);
        merge(arr,begin,end,middle);
    }
}
void merge(int *arr, int begin, int end, int middle)
{
    int i, j, k, c[50];
    i = begin;
    k = begin;
    j = middle + 1;
    while (i <= middle && j <= end)
    {
        if (arr[i] < arr[j])
        {
            c[k] = arr[i];
            k++;
            i++;
        }
        else
        {
            c[k] = arr[j];
            k++;
            j++;
        }
    }
    while (i <= middle)
    {
        c[k] = arr[i];
        k++;
        i++;
    }
    while (j <= end)
    {
        c[k] = arr[j];
        k++;
        j++;
    }
    for (i = begin; i < k; i++)
    {
        arr[i] = c[i];
    }
}

Output:

Enter number of elements to be sorted:8
Enter 8 elements to be sorted:5
9
22
54
1
-8
6
45
Sorted array
-8      1       5       6       9       22      45      54

In the next section of the tutorial, we will discuss the Quick Sort in Data Structure and its concept and the algorithm of Quick Sort for performing different sorting operations in detail. We shall discuss the algorithm and working principle in the same way as done in this article using real-world examples.