In this section of the tutorial, we will discuss the Selection Sort in Data Structure and its concept and the algorithm of Selection Sort for performing different sorting operations in detail. We shall discuss the algorithm and working principle in the same way as done in this article using real-world examples.

Now, let’s move further and understand the definition of Selection Sort in Data Structure.

What is Selection Sort in Data Structure?

In Selection Sort, we sort a list of unordered data item. Here, we select the smallest item and move it in a sorted list. This process continues until the whole is completely sorted.

• A list of unordered data elements is worked upon.
• Smallest item is selected first and it is moved to a sorted list.
• Then the remaining data items are searched for the next smallest item.
• Again the smallest item is moved to the sorted list.
• This process continues until the whole list is sorted.
• In each sort pass, the smallest element is selected from the unsorted sublist.
• Then the selected element is exchanged with the element at the beginning of the unsorted list.

Now, we will understand the concept involved in the Selection Sort.

Concept used in Selection Sort

The concept of sorting in Selection Sort is somewhat similar to the previous sorting techniques we have learnt. We will go through the core concepts in the points given below.

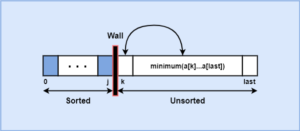
• Initially, the list of unsorted data elements is divided into two sublists, namely sorted and unsorted list.
• Now, a smallest element is selected from the unsorted list and it is exchanged with the element at the beginning of the unsorted list.
• Each time an element is exchanged or moved from the unsorted list to the sorted list, we call it one sort pass.
• After each sort pass, the imaginary wall between the two sublists moves one element to the right, increasing the number of sorted elements and decreasing the number of unsorted elements.
• For n number of elements, there will be n-1 passes to completely sort the entire list of data elements.

Now that we are familiar with the concept involved in the Selection Sort, we will now write down its algorithm before we put it into implementation.

Selection Sort Algorithm

Now, we will have to put the concept into a set of instructions before we actually use a programming language to solve a real problem using it. So, it is important that we write the Algorithm of Selection Sort.

Algorithm Selection_Sort (list, last)
1 set current to 0
2 loop (till last element is sorted)
    1 set smallest element to current
    2 set walker element to current + 1
    3 loop (walker <= last)
        1 if (walker key < smallest key)
            1 set smallest element to walker element
        2 increment walker element
    4 end loop
    5 exchange (current, smallest)
    6 increment current
3 end loop
end Selection_Sort

• Here, we are going to sort an array list of unsorted data elements.
• First, we will select the smallest element from the unsorted sublist.
• Further, we will exchange that selected element with the element at the beginning of the unsorted array list.
• list of data elements must have at least one item in it.
• last contains the index value to the last element in the list.
• After the sorting is completed, the list of data items in the array is arranged in ascending order.

Working of Selection Sort

The working of Selection Sort is very simple. We will look into an example with illustrated diagrams to understand the working of Selection Sort in detail.

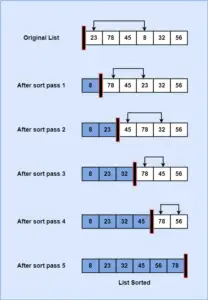
• As a person with no knowledge of sorting, when asked to sort a list of data items, would sort the elements by first checking and selecting the smallest element present in the list.
• Then separately writing it down in another list, and gradually keep adding elements in the sorted list from the unsorted list in ascending order.
• This will eventually sort the entire list of data elements in a particular order(smallest to largest).
• This is the layman’s term of explaining the working principle of the Selection Sort.
• It starts with selecting the smallest item from the unsorted list and keeps on exchanging it with the elements in the sorted list until the elements in the unsorted sublist are empty.

Time and Space Complexity of Algorithm

Selection Sort Implementation

Now that we have understood the concept of Selection Sort and written its algorithm. It’s time to finally implement what we have learnt so far. Here, we will use C and C++ to implement Selection Sort in solving a problem in Data Structure.

Implementation in C

Code:

#include <stdio.h>
int main()
{
    int a[10]={7,1,8,995,41,0,45,73,6,4};
    int n, i, j, temp;
    n=sizeof(a)/sizeof(a[0]);
    for(i = 0; i < n; i++)
    {
        for(j = i + 1; j < n; j++)
        {
            if(a[i] > a[j])
            {
                temp = a[i];
                a[i] = a[j];
                a[j] = temp;
            }
        }
    }
    printf("Sorted List using Selection Sort: ");
    for(i = 0; i < n; i++)
    {
        printf("%d ",a[i]);
    }
    printf("\n");
    return 0;
}

Output:

Sorted List using Selection Sort: 0 1 4 6 7 8 41 45 73 995

Implementation in C++

Code:

#include <iostream>
using namespace std;
int main()
{
    int a[10]={7,1,8,995,41,0,45,73,6,4};
    int n, i, j, temp;
    n=sizeof(a)/sizeof(a[0]);
    for(i = 0; i < n; i++)
    {
        for(j = i + 1; j < n; j++)
        {
            if(a[i] > a[j])
            {
                temp = a[i];
                a[i] = a[j];
                a[j] = temp;
            }
        }
    }
    cout<<"Sorted List using Selection Sort: ";
    for(i = 0; i < n; i++)
    {
        cout<<a[i]<<" ";
    }
    cout<<"\n";
    return 0;
}

Output:

Sorted List using Selection Sort: 0 1 4 6 7 8 41 45 73 995

In the next section of the tutorial, we will learn the Merge Sort and its concept in Data Structure and the algorithm of Merge Sort in detail. We will understand the algorithm and the working principle using a few program examples.