In this section of the tutorial, we will discuss the use of Tree in Data Structure which includes Binary Tree, Binary Search Tree, AVL Tree, B Tree and B+ Tree and some important tree operations as well as its implementation in programs.
Now let’s move on further to the introduction of Tree in Data Structure.
What is Tree in Data Structure?
A tree consists of a finite set of elements in it that are called nodes, and a finite set of directed lines that are called branches that connects the nodes.
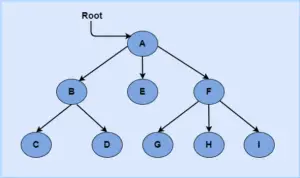
- Trees are studied from a very old time initially to study the structure of algebraic formulas. Now the trees are extensively used in computer science.
- Trees represent algebraical formulas.
- Trees are efficient in performing various data structure operation such as searching of large and dynamic list.
- Trees are also used in diverse applications based on artificial intelligence systems and encoding algorithms.
We will learn the concepts and terminologies of Tree in Data Structure now.
Basic Tree Terminology
- Degree of the node: It is the number of branches associated with a node.
- Indegree branch: In this, the branch is directed toward the node.
- Outdegree branch: In this, the branch is directed away from the node.
- Root: It is the first node of the tree.
- Leaf: It is any node with no successors or node with an outdegree of zero.
- Internal node: It is a node that is not a root or a leaf as it is found in the middle of the tree.
- Parent node: A node that has successor nodes in it or which has an outdegree greater than zero.
- Child node: It is a node that has predecessor in it.
- Siblings: They are two or more nodes having the same parent.
- Path: It is a sequence of nodes where each node is adjacent to the next one.
- Ancestor: It is any node in the path from the root to the node.
- Descendent: It is any node in the path below the parent node.
- Level of a node: It is the distance of the node from the root.
Types of Tree in Data Structure
Although there are many types of Tree structure in Data Structure. Here we will discuss a few like Binary Tree, Binary Search Tree, AVL Tree, B Tree, and B+ Tree.
Binary Tree
In binary tree, the nodes cannot have more than two subtrees. In other words, the maximum outdegree for a node is two.
- Binary tree has subtrees that can be treated as left subtrees and right subtrees.
- Each of these subtree is itself a binary tree in nature.
- Maximum height of binary tree is H(max) = N, where N is the number of nodes in the tree.
- Minimum height of binary tree is H(min) = [log2N] + 1.
- Minimum nodes in binary tree is N(min) = H, where H is the height of the tree.
- Maximum nodes in binary tree is N(max) = 2^H-1.
Binary Search Tree
In a binary search tree, the subtree in the left holds the key values less than the root and the subtree in the right holds the key values greater than or equal to the root.
- All the items in the left subtree are less than the root.
- All items in the right subtree are greater than or equal to the root.
- Each subtree in its individuality is a binary search tree.
Binary Search Tree Operations
These are some basic operations to perform the Binary Search Tree Operations in Data Structure. Although, any other operation can also be carried out and added to the data structure.
Search Operation
This operation searches and locates a specific node in the tree. We will look into the binary search algorithm to understand the working of the search operation.
- BST Search operation can be implemented using recursion.
- There are two base cases in this operation, i.e. either finding the search operation in the tree, in which the address of its node is returned.
- Or the searching argument doesn’t exist in the tree, in which null is returned to the user.
Insert Operation
The insert operation adds data to a binary search tree. All the binary search tree insertion operations take place at a leaf or a leaflike node.
- To insert the data, we must follow the branches to an empty subtree and then insert the new node into it.
- In other words, all inserts happen at a leaf or a leaflike node that has only one null subtree.
- We can use recursion to insert data into the node.
Delete Operation
The delete operation deletes a node from a binary search tree, but it must be located first before deleting.
There can be four situations when we delete a node:
- When the node has no children. Then we simply delete the node.
- When the node has only one right subtree. Then we delete the node and attach the right subtree to the deleted node’s parent.
- When the node has only one left subtree. Then we delete the node and attach the left subtree to the deleted node’s parent.
- When the node has two subtrees. Then we delete the node and find data to take place of the deleted node to avoid any imbalance between the subtrees.
AVL Tree
AVL Trees are balanced by working with their height so they are also known as height-balanced binary search tree.
- AVL Tree is a search tree where the heights of the subtrees differ by no more than 1.
- That is the reason why it is called a balanced binary tree.
- An AVL Tree is a binary tree that is either empty or consists of two AVL subtrees, i.e. T(L) and T(R), whose heights differ by no more than 1.
- The generalised formula deduces by the concept of AVL Tree is |H(L) – H(R)| <= 1.
AVL Tree Operations
These are some basic operations to perform the Binary Search Tree Operations in Data Structure. Although, any other operation can also be carried out and added to the data structure.
Insert Operation
This operation is carried out in the same way as for many binary trees. We use an inorder traversal as we know that AVL Trees are search trees.
- All the insertion takes place at a leaf node.
- We follow the path from the root to find the appropriate leaf node.
- We traverse to left when the new data’s key is less than a node’s key and right is it is otherwise.
- When the leaf is found, we connect it to the parent node.
- Then we back out of the tree while constantly checking the balance of each node.
- If any unbalance node is found, we fix it. And this is how the whole insert operation is performed in AVL Tree.
Delete Operation
This operation deletes the node from a leaf. The same method of checking the node is done when we back out of the tree as we did in the insert operation.
- The operation deletes a node from the AVL Tree and rebalances if necessary.
- If we find a null tree, the node doesn’t exist in the AVL Tree and the deletion is not successful.
B-Tree
A B-tree is a m-way search tree which is perfectly balanced where each node is atleast half full except the root node.
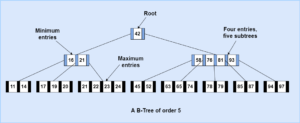
There are various properties of B-Tree such as:
- The root is either a leaf or it has 2…m subtrees.
- All the internal nodes have atleast m/2 non-null subtrees and at most m non-null subtrees.
- All the leaf nodes are at the same level, which makes it a perfectly balanced tree.
- Each leaf node has at least (m/2)-1 entries and at most (m-1) entries.
B+ Tree
B+ Tree are mostly used in situation where the data needs to be processed both randomly and sequentially. B+ Tree is an effective tree that can be used in such operations where the data is very large in quantity.
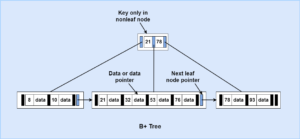
- B+ Tree is much more time-efficient than the B-Tree.
- In B+ Tree, each data entry must be represented at the leaf level.
- Each leaf node has one additional pointer in it that is used to move to next leaf node in the sequence.
- When the data are randomly processed, the tree search is modified to find the target data only at a leaf. This results in a little increase in the search time.
- When the data are sequentially processed, the far-left entry is located and then the data is processed in the same manner as the data are processed in a linked list where each node is an array.
Program examples to demonstrate the implementation of Binary Search Operations
Program to search for a node in a binary tree.
Code:
#include<bits/stdc++.h>
using namespace std;
struct Node{
int val;
Node *left, *right;
};
Node* addNode(int value){
Node* temp = new Node();
temp->val = value;
temp->left = temp->right = nullptr;
return temp;
}
bool findNode(Node * root, int target){
if(root == nullptr) return false;
if(root->val == target) return true;
if(findNode(root->right, target))return true;
return findNode(root->left, target);
}
int main(){
Node* root = addNode(1);
root->left = addNode(2);
root->right = addNode(3);
root->left->left = addNode(4);
root->left->right = addNode(5);
root->left->right->left = addNode(6);
root->right->right = addNode(7);
root->right->right->right = addNode(8);
root->right->right->left = addNode(9);
int ans = findNode(root, 10);
cout<<(ans?"Node found":"Node not found")<<endl;
return 0;
}
Output:
Node not found
Program to find maximum height of a binary tree
Code:
#include <bits/stdc++.h>
using namespace std;
struct Node{
int val;
Node *left;
Node *right;
};
Node* newNode(int data)
{
Node* temp = new Node;
temp->val = data;
temp->left = NULL;
temp->right = NULL;
return(temp);
}
int maxDepth(Node* root) {
if(!root)return 0;
return max(maxDepth(root->left),maxDepth(root->right))+1;
}
int main(){
Node *root1 = newNode(1);
root1->left = newNode(2);
root1->right = newNode(3);
root1->left->left = newNode(94);
root1->left->right = newNode(5);
cout<<"Maximum depth of the tree is: ";
cout<<maxDepth(root1);
}
Output:
Maximum depth of the tree is: 3
Program to find maximum width of a binary tree
Code:
#include <bits/stdc++.h>
using namespace std;
struct Node{
int val;
Node *left;
Node *right;
};
Node* newNode(int data)
{
Node* temp = new Node;
temp->val = data;
temp->left = NULL;
temp->right = NULL;
return(temp);
}
int getMaxElement(Node* root)
{
if (root == NULL)return numeric_limits<int>::min();
int res = root->val;
int lres = getMaxElement(root->left);
int rres = getMaxElement(root->right);
res = max({rres,lres,res});
return res;
}
int main(){
Node *root1 = newNode(1);
root1->left = newNode(2);
root1->right = newNode(3);
root1->left->left = newNode(94);
root1->left->right = newNode(5);
cout<<"Maximum element is: "<<getMaxElement(root1);
}
Output:
Maximum element is: 94
In the next section of the tutorial, we will discuss the use of Graph in Data Structure which will include the types of graph, graph representation, DFS Algorithm, BFS Algorithm, Prim’s Algorithm, Kruskal’s Algorithm and its implementation in programs that will be used thoroughly in this Data Structure tutorial.