How to write a java program that gives a solution for the N-Queens problem. Let’s solve Java challenging problem. First, let us understand what is N-Queens problem.
What is the N-Queens problem?
The N-Queens problem can be described as:
“How can N queens be placed on an N*N chessboard so that no two queens attack each other?”
Before solving the problem, we need to first understand the movement of queens in a chessboard.
A queen can move in any of the following direction:
- along the row in which it is currently placed
- along the column in which it is currently placed
- or along any of the diagonal direction
But the condition is that once it moves in any direction, it can’t change it afterward. So the N queens should be such placed in an N*N chessboard such that none of them can attack each other.
We will solve the N-Queens problem using backtracking.
What is Backtracking?
Backtracking algorithm is a brute-force approach that determines the solution by finding all possible combinations to solve a problem by rejecting the solutions that do not work.
When the solution is not found for a combination, it goes back to the previous step and tries to solve the problem again.
What is the algorithm for the N-Queens Problem?
- We will first create a character array of size N*N and initialize it with ‘-‘.
- First, we will place a queen in a position. If after placing another queen, the previous queen is under attack, then we will try all possible positions for the queen. And if that does not work, we will backtrack to the previous queen and change its position.
- For this, we will create a method named isSafe() which tells whether it is safe to place the queen. The method takes chessboard array, no. of rows, no. of columns as input. The first loop checks whether there is any queen along the row and returns false otherwise returns true. The second and third for loop checks whether there is any queen along the diagonal and returns false otherwise returns true.
- We will create another method named solveNQueens() which is responsible for placing the queens at their appropriate positions. If the method isSafe() returns true for the position, it places the queen. Else it backtracks by marking the previous position of the queen as ‘-‘.
- The method is called recursively to obtain a solution for the n-queens problem.
Java Program for N-Queens Problem:
import java.util.Scanner;
public class NQueens
{
public static void main(String[] args)
{
Scanner sc=new Scanner(System.in);
System.out.println("Enter the value of n");
int n=sc.nextInt();
char board[][]=new char[n][n];
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
board[i][j]='-';
if(solveNQueens(board,0,n)) solution(board,n);
else System.out.println("No solution exists");
}
public static void solution(char board[][], int n)
{
for(int i=0;i<n;i++)
{
for(int j=0;j<n;j++)
System.out.print(" "+board[i][j]+" ");
System.out.println();
}
}
public static boolean isSafe(char board[][], int row, int column, int n)
{
int i,j;
for(i=0;i<column;i++)
{
if(board[row][i]=='Q') return false;
}
for(i=row,j=column; i>=0 && j>=0;i--,j--)
{
if(board[i][j]=='Q') return false;
}
for(i=row,j=column; i<n && j>=0;i++,j--)
{
if(board[i][j]=='Q') return false;
}
return true;
}
public static boolean solveNQueens(char board[][], int column, int n)
{
if(column>=n) return true;
for(int i=0;i<n;i++)
{
if(isSafe(board,i,column,n))
{
board[i][column]='Q';
if(solveNQueens(board, column+1,n)) return true;
board[i][column]='-';
}
}
return false;
}
}
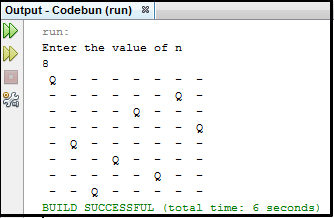
Output for the N-Queens Problem: