Divide and Conquer in Data Structure

In this tutorial, we will learn about the Divide and Conquer Method that is used in solving problems in Data Structure. We will learn how the algorithm based on this method works, where we can use the Divide and Conquer method, what are the application of this method with some good examples.

Now, let’s move on to the introductory definition of the Divide and Conquer Method.

What is Divide and Conquer Method?

The divide and conquer method is a powerful approach to organize the problems into subproblems that are expressed naturally in a recursive way. This is the same approach that we have discussed in the previous section while representing an algorithm of a problem.

This strategy helps in solving big and complex problems by dividing it into multiple subproblems and then merging it once the problem is solved.
This divide and conquer method improves the programmability of many problems that fits in this pattern, while providing a similar performance.
This overall boosts up the efficiency of the program to solve a particular problem.
The divide and conquer method is often used in big and complex programs.
It is used whenever we want to compute a solution to a problem by dividing it into smaller subproblems.
These subproblems are solved individually, and later the subsolutions are merged into a global solution for the initial problem.
The divide and conquer method is used recursively to the subproblems until a base or indivisible form of the problem is encountered.
The divide and conquer method is often regarded as the basic skeletons of solving a problem in the data structure.

Now, we will look into an example to understand what this Divide and Conquer method is all about.

Example: Demonstrate the use of the Divide and Conquer Method while solving the Fibonacci Series problem.

int fib(int n)
{
if (n < 2) return n;
else return fib(n − 1) + fib(n − 2);
}

Here, the basic elements of the divide and conquer method are:

Identifying the base case or indivisible subproblem (n<2).
The solving of the subproblem.
The partition in several subproblems otherwise the function will return fib(n − 1) and fib(n − 2).
Finally, when all the subproblems are solved, the results of each subproblem are combined or merged to obtain the overall solution for the initial problem, i.e. Fibonacci Series.

This is the simplest implementation of the Divide and Conquer method in solving a problem. Further, we will discuss more problems and we will understand the approach of solving them by divide and conquer method.

Working of Divide and Conquer Method

As we have discussed above, the working of the Divide and Conquer Method requires splitting a problem into smaller subproblems and then solving each subproblem to find a subsolution and then eventually all the subsolutions are summed up into a single solution for the given problem.

Now, we will understand its working with the help of few examples.

Example: To demonstrate the working of Divide and Conquer Method for sorting a set of values.

Algorithm Sort (S)

if |S| ≤ 1 then return S

else divide (S, S1, S2)

     fusion (sort (S1), sort (S2))

end if

end Algorithm

Here, fusion is linear, it is the size of its parameter.
divide is either in O(1) or O(n).
The output will be O(nlogn).

In solving the above problem, we followed a set of rules:

Finding the size of the problem (say) n.
Then we divide the problem into smaller subproblems of size n/b.
This adds a linear complexity of cn.
Then we sort each subproblem and the compute subsolution.
Eventually, we sum up the terms together that will give the sorted values as the end result.

Now we will understand how the divide and conquer method works for sorting values with the help of illustrated diagrams below.

Step 1: Finding the size of elements

Step 2: Dividing the elements into smaller subproblems of equal sizes

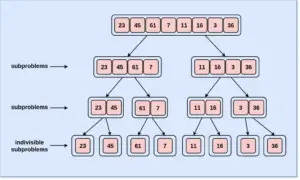
Step 3: Sorting each subproblem individually to obtain subsolutions

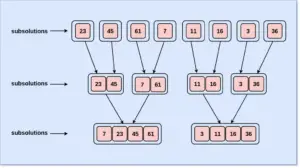
Step 4: Merging the subsolutions into a single form to obtain the desired output

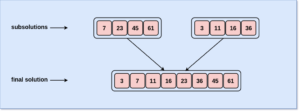
This approach of dividing the problems and solving them separately makes it easy to solve any given problem with ease at a better efficiency.

Why do we use Divide and Conquer Method?

There are many advantages of using Divide and Conquer Method in solving a problem. By now, we must have an idea of how it is used and applied to solve a complex problem.

Now, we will discuss a few points that tell us how the divide and conquer method is useful for a developer.

Divide and conquer method is based on splitting a big problem into many small subproblems.
These subproblems are solved directly one by one.
After each of them is solved, all the subsolutions are merged or integrated into one single form to get the desired output.
While using this method, the concept of recursion is extensively used in repeating the same algorithm to solve all the subproblems.
This method is used in multiprocessing systems.
While using this method to solve a problem, the memory cache used in the operations is used efficiently.
For example, operation on matrices, Tower of Hanoi algorithm, sorting and searching operation, and so on, can be solved using the divide and conquer method.

We will further discuss the application of Divide and Conquer Method as it is most often used in programming.

Applications of Divide and Conquer Method

There are many operations in Data Structure that can be implemented using Divide and Conquer Method, some of which are:

In Searching techniques, the divide and conquer method can be implemented on Binary search operation.
In Sorting techniques, the divide and conquer method can be implemented on Quick Sort and Merge Sort operations.
In Matrix operations, the divide and conquer method can be implemented on Strassen’s Matrix multiplication.
Also, the divide and conquer method can be implemented along with Karatsuba Algorithm.

In the next section of the tutorial, we will discuss the use of Pointer in Data Structure and we will understand how Pointer improves the overall performance in recursive operations in a program.