In this section of the tutorial, we will discuss the Quick Sort in Data Structure and its concept and the algorithm of Quick Sort for performing different sorting operations in detail.

Now let’s move further to the introduction of Quick Sort in Data Structure.

What is Quick Sort in Data Structure?

In Quick Sort, data elements present in the form of arrays are divided further into smaller arrays, and then it is called recursively to sort the smaller arrays.

We will understand the division of list into different partitions with the help of an illustrated diagram.

• Each iteration, an element is selected called pivot. This pivot divides the list of elements into three parts.
• First part contains the elements having keys less than the pivot’s key.
• Second part contains the pivot element that is placed at the correct location in the list.
• Third part contains the elements having keys greater than or equal to the pivot’s key.
• The sorting of elements starts recursively twice, one from quick sorting the left part and one from quick sorting the right part.

Now we will understand the concept involved in Quick Sort.

Concept used in Quick Sort

The concept of Quick Sort was first proposed by C. A. R. in 1962. We will understand the concept of Quick Sort with the help of illustrated diagrams.

• It was more efficient in sorting a list of elements than other exchange sorts such as Bubble Sort.
• The concept revolves around following an algorithm where a pivot key is selected as the first element in the list that is the median position of the three elements’ location, i.e. left, right, and middle of the list.
• Then the determined median value is exchanged with the left element of the list.
• The selected pivot key is placed in its correct position in the array while sorting the other elements present in the left and right part of the list.

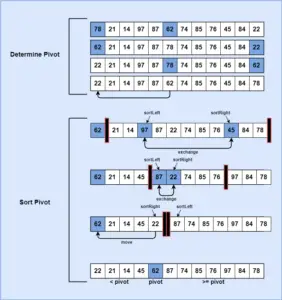
• Here, before the exchange takes place, the median element lies in the middle position.
• The smallest element among the three determines whether the median is in the right location.
• Then after calling the median left algorithm, the median is in the left part and the smallest element is in the middle.
• The pivot key is then moved out temporarily until the sort is processed. This put the pivot key in the correct location in the list.

Quick Sort Algorithm

Now that we are familiar with the concept of Quick Sort, we can now develop an algorithm of Quick Sort before we put it into implementation.

Algorithm QuickSort (list, left, right)
1 if ((right - left) > min_size)
    1 median_left (list, left, right)
    2 set pivot to left element
    3 set sort_left to left + 1
    4 set sort_right to right
    5 loop (sort_left <= sort_right)
        1 loop (sort_left key < pivot key)
            1 increment sort_left
        2 end loop
        3 loop (sort_right key >= pivot key)
            1 decrement sort_right
        4 end loop
        5 if (sort_left <= sort_right)
            1 exchange(list, sort_left, sort_right)
            2 increment sort_left
            3 decrement sort_right
        6 end if
    6 end loop
    7 move sort_left - 1 element to left element
    8 move pivot element to sort_left - 1 element
    9 if (left < sort_right)
        1 QuickSort (list, left, sort_right - 1)
    10 end if
    11 if (sort_left < right)
        1 QuickSort (list, sort_left, right)
    12 end if
2 else
    1 InsertionSort (list, left, right)
3 end if
end QuickSort

Working of Quick Sort

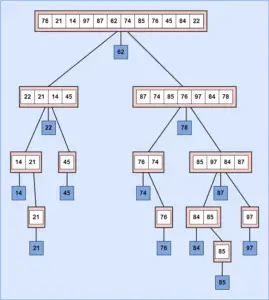
• Here, an array list is sorted using Quick Sort algorithm.
• Quick Sort is called recursively twice to solve the list of elements.
• list is an array of elements to be sorted by the algorithm.
• left and right specify the first and last element present in the list.
• loop is iterated to find the key on left that belongs to right.
• Another loop is iterated to find the key on right that belongs to left.
• Each time for a sort pass the above steps takes place, the iteration of loops and exchanging of elements takes place until the list is sorted completely.

In the diagram given below, Quick Sort is used to sort the list of array elements.

Time and Space Complexity of Algorithm

Quick Sort Implementation

Now that we understand the concept of Quick Sort and also we have written the algorithm of Quick Sort, now we can implement Quick Sort in a programming language to perform the operation. Here, we will implement the Quick Sort in C and C++.

Implementation in C

Code:

#include <stdio.h>
void quick_sort(int [], int, int);
int split(int [], int, int);

int main()
{
    int arr[8] = {21, 82, 73, 17, 35, 58, 64, 49};
    quick_sort(arr, 0, 7);
    for (int i = 0; i < 8; i++)
    {
        printf("%d ",arr[i]);
    }
    printf("\n");
    return 0;
}

void quick_sort(int a[], int start, int end)
{
    if (start < end)
    {
        int mid = split(a, start, end);
                        quick_sort(a, start, mid - 1);
                        quick_sort(a, mid + 1, end);
    }
}

int split(int a[], int start, int end)
{
    int temp;
    int x = a[end];
    int i = start - 1;
    for (int j = start; j < end; j++)
    {
        if (a[j] <= x)
        {
            i++;
            temp = a[i];
            a[i] = a[j];
            a[j] = temp;
        }
    }
    temp = a[i+1];
    a[i+1] = a[end];
    a[end] = temp;

    return i+1;
}

Output:

17 21 35 49 58 64 73 82

Implementation in C++

Code:

#include <iostream>
void quick_sort(int [], int, int);
int split(int [], int, int);

int main()
{
    int arr[8] = {21, 82, 73, 17, 35, 58, 64, 49};
    quick_sort(arr, 0, 7);
    for (int i = 0; i < 8; i++)
    {
        std::cout << arr[i] << " ";
    }
    std::cout << "\n";
    return 0;
}

void quick_sort(int a[], int start, int end)
{
    if (start < end)
    {
        int mid = split(a, start, end);
                        quick_sort(a, start, mid - 1);
                        quick_sort(a, mid + 1, end);
    }
}

int split(int a[], int start, int end)
{
    int x = a[end];
    int i = start - 1;
    for (int j = start; j < end; j++)
    {
        if (a[j] <= x)
        {
            i++;
            std::swap(a[i], a[j]);
        }
    }
    std::swap(a[i+1], a[end]);

    return i+1;
}

Output:

17 21 35 49 58 64 73 82

In the next section of the tutorial, we will discuss the Heap Sort in Data Structure and its concept and the algorithm of Heap Sort for performing different sorting operations in detail. We shall discuss the algorithm and working principle in the same way as done in this article using real-world examples.